How to Convert and Calculate Percentage?

How to convert to Percentage: Best and Simple Ways

The ability to convert numbers, fractions and decimals into percentages is necessary knowledge for many industries, including engineering, economics and business.

Understanding and calculating percentages can help you in many ways: working out the correct tip at a restaurant, knowing how much you are saving on that mega sale or allowing you to interpret data from mathematical and scientific research. In short, learning more about percentages is important for chemistry and all other areas.

A percentage is a way of expressing one number as a portion or share of a whole number, and percentages are always based on their relation to 100, which represents the whole number or object. For example, 75% is the same as 75 out of 100. Any percentage lower than 100 is just part of the whole or total.

Check out the guide below on how to convert numbers, fractions and decimals into percentages in easy and simple ways.

What is a Percentage?

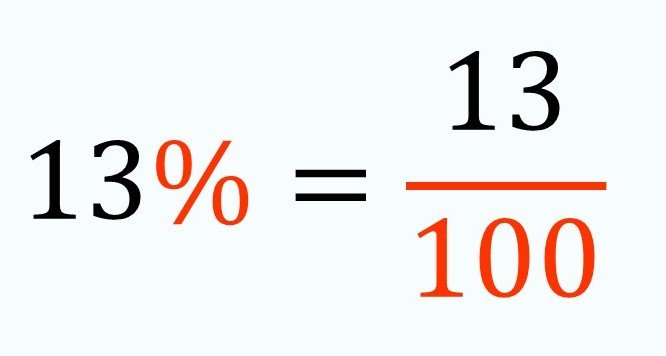Photo: Smartick

The term ‘per cent’ means ‘out of a hundred’. In mathematics, percentages are used like fractions and decimals, as ways to describe parts of a whole. When you are using percentages, the whole is considered to be made up of a hundred equal parts. The symbol % is used to show that a number is a percentage, and less commonly the abbreviation ‘pct’ may be used.

History

In Ancient Rome, long before the existence of the decimal system, computations were often made in fractions in the multiples of 1/100. For example, Augustus levied a tax of 1/100 on goods sold at auction known as centesima rerum venalium. Computation with these fractions was equivalent to computing percentages.

As denominations of money grew in the Middle Ages, computations with a denominator of 100 became increasingly standard, such that from the late 15th century to the early 16th century, it became common for arithmetic texts to include such computations. Many of these texts applied these methods to profit and loss, interest rates, and the Rule of Three. By the 17th century, it was standard to quote interest rates in hundredths.

The term "percent" is derived from the Latin per centum, meaning "hundred" or "by the hundred". The sign for "percent" evolved by gradual contraction of the Italian term per cento, meaning "for a hundred". The "per" was often abbreviated as "p."—eventually disappeared entirely. The "cento" was contracted to two circles separated by a horizontal line, from which the modern "%" symbol is derived.

Visualising Percentages

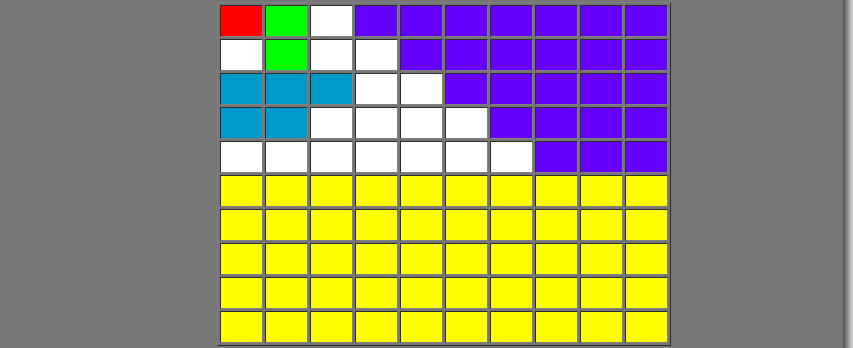
The grid below has 100 cells.

Photo: Screenshot

• Each cell is equal to 1% of the whole (the red cell is 1%).
• Two cells are equal to 2% (the green cells).
• Five cells are equal to 5% (the blue cells).
• Twenty five cells (purple cells) are equal to 25% of the whole or one quarter (¼).
• Fifty cells (yellow cells) are equal to 50% of the whole or half (½).

How many unshaded (white) cells are there? What is the percentage of unshaded cells?

Answer: There are two ways to work this out.

Count the white cells. There are 17 of them. Out of 100 cells, 17% are therefore white.

Add up the number of other cells, and take them from 100. There is one red cell, two green, five blue, 25 purple, and 50 yellow. That adds up to 83. 100−83 = 17. Again, out of 100 cells, 17 are white, or 17%.

It is easy to work out the percentage when there are 100 individual ‘things’ making up the whole, as in the grid above. But what if there are more or less?

The answer is that you convert the individual elements that make up the whole into a percentage. For example, if there had been 200 cells in the grid, each percentage (1%) would be two cells, and every cell would be half a percent.

We use percentages to make calculations easier. It is much simpler to work with parts of 100 than thirds, twelfths and so on, especially because quite a lot of fractions do not have an exact (non-recurring) decimal equivalent. Importantly, this also makes it much easier to make comparisons between percentages (which all effectively have the common denominator of 100) than it is between fractions with different denominators. This is partly why so many countries use a metric system of measurement and decimal currency.

Finding the Percentage

The general rule for finding a given percentage of a given whole is:

Work out the value of 1%, then multiply it by the percentage you need to find.

This is easiest to understand with an example. Let’s suppose that you want to buy a new laptop computer. You have checked local suppliers and one company has offered to give you 20% off the list price of £500. How much will the laptop cost from that supplier?

In this example, the whole is £500, or the cost of the laptop before the discount is applied. The percentage that you need to find is 20%, or the discount offered by the supplier. You are then going to take that off the full price to find out what the laptop will cost you.

1. Start by working out the value of 1%

One percent of £500 is £500 ÷ 100 = £5.

2. Multiply it by the percentage you are looking for

Once you have worked out the value of 1%, you simply multiply it by the percentage you are looking for, in this case 20%.

£5 × 20 = £100.

You now know that the discount is worth £100.

3. Complete the calculation by adding or subtracting as necessary.

The price of the laptop, including the discount, is £500−20%, or £500−£100 = £400.

Once you have calculated 1% of the whole, you can then multiply your answer to the percentage you are looking for.

How to turn a number into a percentage

To turn a number (either an integer or a decimal) into a percent, simply multiply by 100. That is the same as moving the decimal point two places to the right. You may need to round to the desired precision. Add a percent (%) sign.

0.32 as a percent is 32%

38.59 = 3859%

0.002 = 0.2%

To turn a percent into an integer or decimal number, simply divide by 100. That is the same as moving the decimal point two places to the left. Take off the percent (%) sign.

50% as a decimal is 0.50

3.5% = 0.035

250% = 2.50

2. What are Decimals?

Decimals are a set of numbers written together with a dot in between them that is called a decimal point. The numbers to the left of the decimal point are the integers or whole numbers and the numbers to the right of the decimal point are called decimal numbers. If we go right from the ones' place, the next place will be (1/10) times smaller, which will be (1/10)^th or one-tenth position.

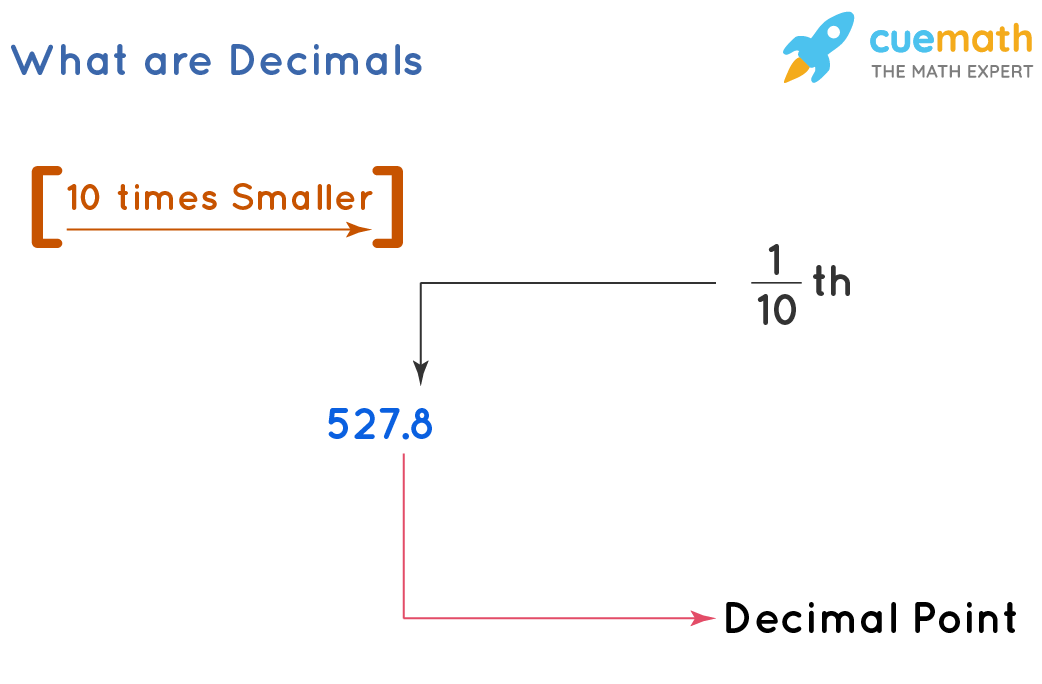Photo: Cuemath

In the case of decimals, for the whole number part, the place value system is the same as the whole number. But after the decimal point, there is a different world of numbers going on in which we use decimal fractions to represent the value. When we are going towards the left, each place is ten times greater than the previous place digit. So, to the right of one's place, we have tenths (1/10) and to the right of tenths, we have hundredths (1/100), and so on. Let us look at some examples for more clarity.

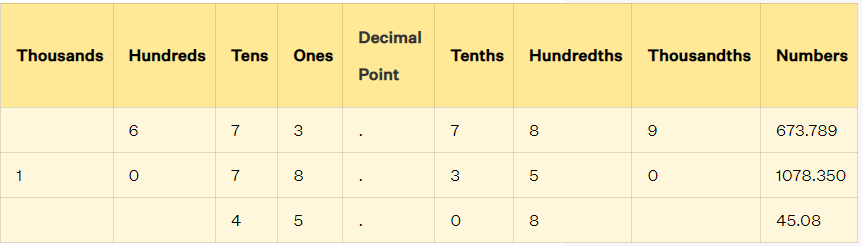Photo: Cuemath

Reading Decimal Numbers: There are two ways to read a decimal number. The first way is to simply read the whole number followed by "point", then to read the digits in the fractional part separately. It is a more casual way to read decimals. For example, we read 34.56 as thirty-four point fifty-six. The second way is to read the whole number part followed by "and", then to read the fractional part in the same way as we read whole numbers but followed by the place value of the last digit. For example, we read 34.56 as thirty-four and fifty-six hundredths.

Writing Decimals: Let us understand this with an example. We have to write the number 123.456 as words. The above decimal number can be written in words as, One hundred twenty-three and four-hundredth fifty-six thousandth, or one hundred twenty-three point four five six. For example, let us try to find out how the decimal number 85.64 can be written in words.

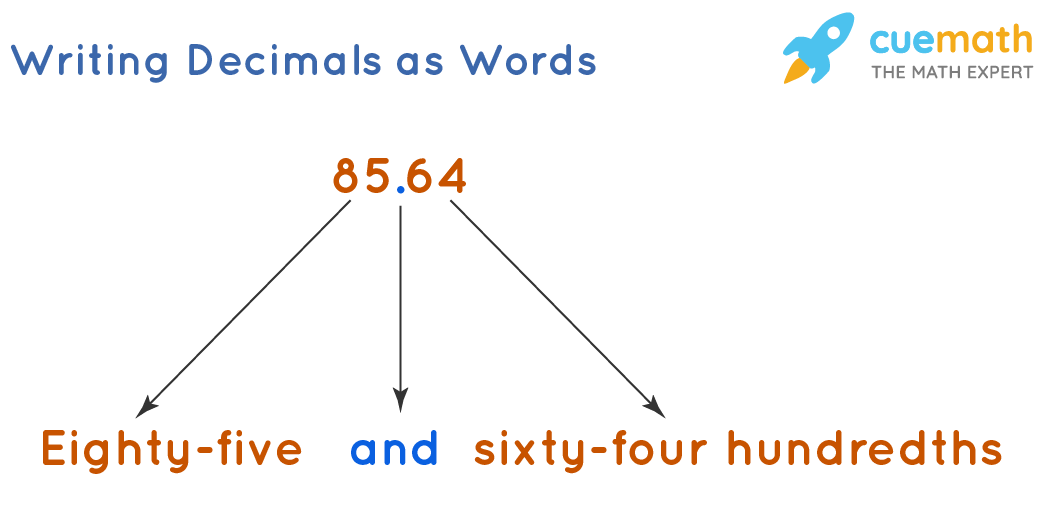Photo: Cuemath

Types of Decimals Decimals can be divided into different categories depending upon what type of digits occur after the decimal point. It will depend upon whether the digits are repeating, non-repeating, end, or un-ending (infinite digits after the decimal point). Let us have a look at how the decimals are categorized based on their type here. Terminating decimals: Terminating decimals mean it does not reoccur and end after a finite number of decimal places. For example: 543.534234, 27.2, etc. Non-terminating decimals: It means that the decimal numbers have infinite digits after the decimal point. For example, 54543.23774632439473747..., 827.79734394723... etc. The Non-Terminating decimal numbers can be further be divided into 2 parts: Recurring decimal numbers: In Recurring Decimal Numbers, digits repeat after a fixed interval. For example, 94346.374374374..., 573.636363... etc, Non- recurring decimal numbers: Non- Recurring Decimal Numbers, digit never repeat after a fixed interval. For example 743.872367346.., 7043927.78687564... and so on.

How to turn Decimals to Percentages

Photo: Math- only

Decimals are even easier to convert into percentages. To convert a decimal into a percentage, multiply the decimal by 100 and add the percent sign. To multiply a decimal by 100, move the decimal point two digits to the right:

0.8= 0.8 x 100 = 80%

0.53: 0.53 x 100 = 53%

0.173: 0.173 x 100 = 17.3%

You can also use this method to convert decimal numbers that are larger than 1. Say you know there are 1.34 times as many books in your library this year than last year, and you want to know what percentage the number of books you have this year is of the books you had last year. As before, you would multiply 1.34 by 100 and add the percent sign:

1.34 x 100 = 134%

Your number exceeds 100 percent because you're comparing this year's book total to the total books from last year, a number represented by 100 percent. Since there are more books this year, that percentage is larger than 100.

Percents Into Decimals

You can convert percentages to decimals using the opposite operation. Instead of multiplying the decimal by 100, divide the percent by 100. If 56 percent of people eat roast beef sandwiches you could also say that for every 100 people, 56 eat roast beef. Divide 56 by 100. Because you're dividing by 100, you'll move the decimal point two places to the left:

56/100 = 0.56

Other conversion examples are: 5%: 5/100 = 0.05, 79%: 79/100 = 0.79, 295%: 295/100 = 2.95

3. What are Fractions?

The word fraction is derived from the Latin word "fractio" which means 'to break'. The Egyptians, being the earliest civilization to study fractions, learned fractions to resolve their mathematical problems, which included the division of food, supplies, and the absence of a bullion currency.

In Mathematics, fractions are represented as a numerical value, can be defined as the parts of a whole. A fraction can be a portion or section of any quantity out of a whole, where, the whole can be any number, a specific value, or a thing. Let us understand this concept using an example. Here's a pizza that is divided into 8 equal parts. Do you know what 1/8 means?

It means one in eight equal parts. It can also be read as:

• One-eighth, or
• 1 by 8

This is called a fraction.

Photo: Cuemath

Parts of a Fraction

All fractions consist of a numerator and a denominator.

• The denominator indicates how many parts the whole has been divided into. It is placed in the lower part of the fraction.
• The numerator indicates how many sections of the fraction are represented. It is placed in the upper part of the whole.

Types of Fractions

Based on numerator and denominator, which are parts of a fraction, there are different types of fractions and those are listed below:

Proper Fraction

Proper fractions are the fractions in which the numerator is less than its denominator. It is often smaller than the whole. Example: 5/7, 3/8, 2/5, etc.

Improper Fraction

An Improper fraction is the type of fraction in which the numerator is more than or equal to its denominator. It is always the same or greater than the whole. Example: 4/3, 5/2, 8/5, etc.

Unit Fraction

Fractions with numerator as 1 are known as unit fractions. Example: 1/4, 1/7, 1/9, etc.

Mixed Fraction

A mixed fraction is a mixture of a whole and a proper fraction. Example: 513513, 225225, 79117911, etc.

Equivalent Fraction

Equivalent fractions are the fractions that represent the same value. It's the same portion of a whole. To get equivalent fractions of any given fraction:

• We can multiply both the numerator as well as the denominator of the given fraction by the same number.
• And for division, we can divide both the numerator and the denominator of the given fraction by the same number.

Example: Find the two fractions equivalent to 5/7.

Solution:

Equivalent Fraction 1: 5/7= 5/7 × 2/2 = 10/14

Equivalent Fraction 2: 5/7 = 5/7 × 3/3 = 15/21

Like and Unlike Fractions

Like fractions are the fractions that have the same denominators. Example: 5/15, 3/15, 17/15, and 31/15.

Unlike fractions are the fractions which have different denominators. Example: 2/7, 9/11, 3/13, and 39/46.

How to Convert a Fraction to Percent?

To convert fraction to a percent, you only need to follow the two simple steps below:

• First, convert the given fraction into a decimal. Use long division method to divide the numerator by the denominator
• Multiply the resultant decimal by 100.
• It should be noted the result is written followed by the percentage sign (%) behind.

In order to understand the process well, let’s solve a few examples by applying the above steps.

Example 1

Convert 3/4 to a percent.

Explanation

• Begin by converting the fraction 3/4 into decimal.
• Divide the numerator by the denominator: 3 ÷ 4 = 0.75
• Multiply the decimal by 100 and write the result with the percentage sign: 0.75 × 100 = 75%.
• Therefore, 3/4 = 75%

Example 2

Convert 3/16 to per cent.

Explanation

• Convert 3/16 into decimal by dividing the numerator by the denominator
• 3 ÷ 16 = 0.1875
• Now multiply the decimal number by 100 and write the result followed by percentage symbol (%): 0.1875 × 100 = 18.75%
• Therefore, 3/16 = 75 %

Other examples of conversion of fractions to percent are:

1. 3/25 = (0.12 × 100) % = 12 %
2. 4/5 = (0.8 × 100) % = 80 %

• 3/4 = (0.75 × 100) % = 75 %

1. 2/3 = (2/3 × 100) % = 0.67 %
2. 1 = (1 × 100) % = 100 %

How to Convert Percent to fraction?

Conversion of percent to fraction is another straight forward operation. You only need to follow the steps outlined below in this article:

• Remove the percentage sign (%) from the given number.
• Write the number as the numerator and 100 as the denominator
• Simplify the fraction, if possible, in its lowest terms.

Let’s also solves some examples by using the steps:

Example 3

Convert 13% to fraction.

Explanation

• Remove the percentage sign (%) and divide the number by 100.
• 13% = 13÷100 = 13/100
• This cannot be simplified and so, the answer is 13/100

Example 4

Convert 2.5% to a fraction.

Explanation

• Remove the percentage sign (%).
• In this case, the given percentage is a decimal number. We just use the same steps but now count number of decimal places and multiply by 100 in powers of 10.
• 5 has 1 decimal place, therefore the power of 10 will be 10 ¹.
• Take the number as a whole number and divide by the product of 100 and 10 ¹.

= 25/ (100 x 10¹) = 25/1000

• The fraction can be simplified into the lowest terms; 25/1000 = 1/ 40.
• Therefore, 2.5% = 1/40

Example 5

Convert 0.005% to fraction.

Explanation

• Remove the percentage sign (%)
• Count the number of decimal places in the number. In this case, 0.005 has 3 decimal places.
• Write the number as a whole number and divide by the product of 100 and 10³.

= 5/ (100 x 10 ³)

= 5/100000

• Reduce the fraction: 5/100000 = 1/20000
• Therefore, 0.005% = 1/20000

Other examples of conversion of percent to fraction:

1. 62 % = 62/100 = 31/50
2. 30 % = 30/100 = 3/10

• 0.5 % = 5/10 % = 5/10 × 1/100 = 1/200

30. 30.2% = 322/10 % = 322/10 × 1/100 = 322/1000 = 151/500
31. 0.4 % = 4/10 % = 4/10 × 1/100 = 4/1000 = 1/250
32. 3²/₅% = 17/5 % = 17/5 × 1/100 = 17/500

• 2/5 % = 2/5 × 1/100 = 1/250
• 16²/₃ % = 50/3 % = 50/3 × 1/100 = 50/300 = 1/6

How to Calculate Percentage using Computer’s Calculator

Step # 1 – Percentage Increases

First you need to open the calculator program, make sure it is in the standard (not scientific) view. As you can see here it is. The first calculation we are going to look at is how to add a percentage amount to a figure, for example 100 +10% of that figure. To do this you need to enter “100” then click the add key and then enter “10” and click the percent key. This will convert the sum to “100+10” which is clearly correct, just click the equals sign to complete the sum.

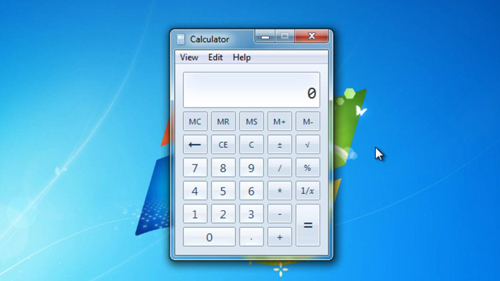Photo: Screenshot

Step # 2 – Percentage Decreases

Now that you know how the percentage key works for an increase it is fairly logical how a decrease works. For example let’s say we want to reduce 80 by 10%, enter “80” then click minus then click “10” and then the percentage key. Finally click equals and the result will appear, here, “72”.

Step # 3 – Combination of Percentages

Let’s have a look at how we can combine these percentage calculations with a real world example. Let’s say we have a bicycle for sale for $1000, it is on sale by 40%, but it also attracts a sales tax of 20%. Working out the final price with calculator is very easy. Enter the original price, here 1000, then minus “40” with the percent button, then you need to add the tax so click the plus key then type 20 and then the percentage sign. Finally click the equals key and you will be given your final cost, here that is $720 – which is correct. You now know how to calculate percentage using Windows calculator.

Calculation of the percentage on the Android mobile

Android calculator

If you prefer to calculate the percentage using the Android calculator, know that to do this you simply need to multiply the starting number by the percentage number and divide the result by 100.

Say, for example, you want to calculate 25% of 500. To do this, you need to multiply the initial number (in this case 500 ) For him percentage number (in this case 25 ) using the button (X). After that you have to divide the result obtained (in this case 12,500 ) for 100 and by touching the button (=), you will get the percentage calculation (in the example 125 ).

In the default calculator of many Android devices, there is also a specific function to calculate the percentage. To use it, you must write the starting number, press the button (%) that is present in the menu that can be recalled by pressing the button (<) located to the right, type the percentage number and, if necessary, press thebutton. (=).

IOS Calculator

Photo: The Verge

Application Calculator present "standard" in iPhone allows you to calculate the percentage in an extremely easy and fast way. For this you have to do what I have already told you in the previous lines, that is, multiply the initial number by the percentage and then divide the result by 100.

I will give you a practical example so that you can better understand how to proceed. Suppose you want to calculate 12% of 650. To do this, you must multiply the initial number (in our example 650 ) For him percentage number (Thus 12 ) by pressing the button with the symbol (X). Next, divide the result obtained (in this case 7.800 ) for 100 and by touching the button (=), you will get the percentage calculation (in this case 78 ).

Crab

A fairly quick and easy way to calculate the percentage on iPhone is to use Crab, the 'standard' built-in voice assistant on iOS. To do it, in fact, all you have to do is run it and then say the voice command: » Calculate the [number percentual]% of [number of partenza] "(E.g."Find 20% of 58").

I remind you that you can call Siri by holding down the Start button (At iPhone 8 / 8 Plus and above) by holding down the side button en iPhone X and later models or by the voice command «Hey Siri!«(If you have activated the function Enable "Hey Siri" give him configurations iOS and if your device supports this function).

How to Convert Centimeters to Inches With Easy Steps There are many tools helping you convert inches to centimeters on the web. However, the formula for the conversion is important for you to remember. ...

How to Convert and Download Audible Audiobooks Audible Audiobooks can be convenient for busy people and book lovers, who want to both listen to a book, podcasts and do their works at ...

How to Convert CDA to MP3 and MP3 to CDA: Best Ways to Change You have a CD and want to convert it into MP3? Follow our simple steps to convert successfully.

How to Convert Seconds to Minutes: Simple Ways to Change All of us know one minute is 60 seconds. What formula should we remember to convert seconds to minutes? Follow our simple steps right below!