How to Convert Within Metric Measurements: Check Best Methods and Easy Steps
 |
| Illustrated picture. Photo: Mixi's |
The metric system is a comprehensive system of measurements used in almost all of the world today, the only exception being that of the United States, who uses a different form of standard measurement. One of the biggest advantages that the metric system offers is that conversion between its units is simple, as its units scale by powers of 10.
What Is the Metric System?
Based on the meter for length and kilogram for mass, the metric system was first adopted in France in 1795. After the French Revolution, the government asked scientists to look into replacing thousands of different traditional measurement systems with one that could unify the country. The meter was developed by measuring one-ten-millionth of the quadrant of Earth’s circumference running from the North Pole to the equator, through Paris. The new unit, equal to about thirty-nine inches, was called a meter, and all measurements were based upon it.
The metric system, or SI (Système International), is based off this original meter and currently the official system of measurement for almost all countries, including the countries of the former British Empire, such as Australia. (Canada converted to the metric system in the ’70s and ’80s.) The SI units—fundamental units not based on any other units—are meter, kilogram, second, ampere (electricity), Kelvin (although Celsius is a more practical measurement for nonscientific applications), mole (chemistry), and candela (luminous intensity).
The metric system is a system of measurement that uses the meter, liter, and gram as base units of length (distance), capacity (volume), and weight (mass) respectively.
To measure smaller or larger quantities, we use units derived from the metric units
 |
| Photo: splashlearn |
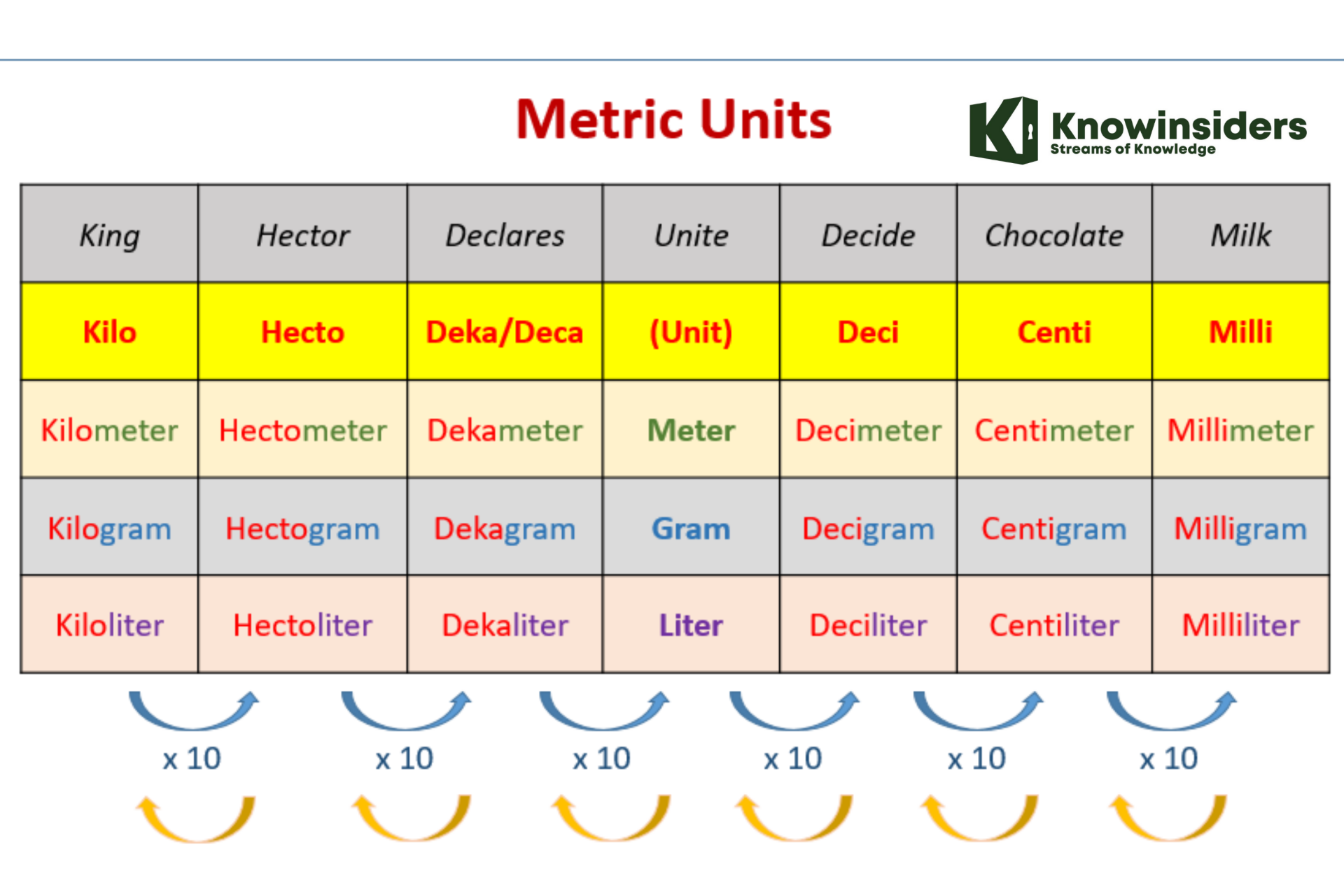
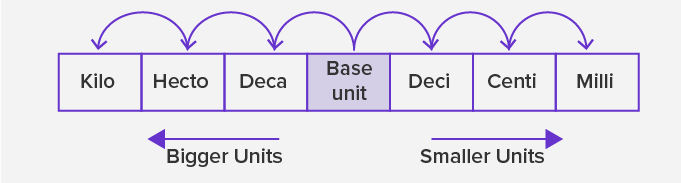
The given figure shows the arrangement of the metric units, which are smaller or bigger than the base unit.
* The units to the right of the base unit are smaller than the base unit. As we move to the right, each unit is 10 times smaller or one-tenth of the unit to its left. So, a ‘deci’ means one-tenth of the base unit, ‘centi’ is one-tenth of ‘deci’ or one-hundredth of the base unit and ‘milli’ is one-tenth of ‘centi’ or one-thousandth of the base unit.
* The units to the left of the base unit are bigger than the base unit. As we move to the left, each unit is 10 times greater than the unit to its right. So, a ‘deca’ means ten times of the base unit, ‘hecto’ is ten times of ‘deca’ or hundred times of the base unit and ‘killo’ is ten times of ‘hecto’ or thousand times of the base unit.
| Kilo | Hecto | Deca | Base Unit | Deci | Centi | Milli |
| 1000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1000 |
So, the units for length, weight (mass) and capacity(volume) in the metric system are:
Length: Millimeter (mm), Decimeter (dm), Centimeter (cm), Meter (m), and Kilometer (km) are used to measure how long or wide or tall an object is.
Examples include measuring the thickness or length of debit card, length of cloth, or distance between two cities.
| Kilometer (km) | Hectometer (hm) | Decameter (dam) | Meter (m) | Decimeter (dm) | Centimeter (cm) | Millimeter (mm) |
| 1000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1000 |
Weight: Gram (g) and Kilogram(kg) are used to measure how heavy an object, using instruments.
Examples include measuring weight of fruits or, our own body weight.
| Kilogram (kg) | Hectogram (hg) | Decagram (dag) | Gram (g) | Decigram (dg) | Centigram (cg) | Milligram (mg) |
| 1000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1000 |
Capacity: Milliliter (ml) and Liter (l) are used to measure how much quantity of liquid an object can hold.
Examples include measuring the amount of juice in a juice can, or amount of water of in a water tank.
| Kiloliter (kl) | Hectoliter (hl) | Decaliter (dal) | Liter (l) | Deciliter (dl) | Centiliter (cl) | Milliliter (ml) |
| 1000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1000 |
Time: Second is the base unit for time. The other metric units of time are:
 |
| Photo: splashlearn |
Convert Within Metric Measurements
Method 1: Converting Through Multiplication and Division
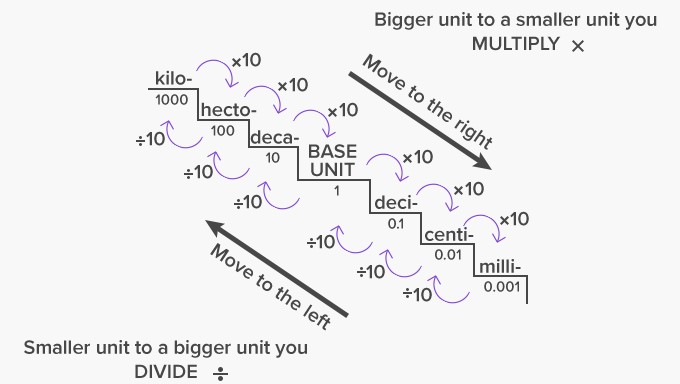
Step 1: Learn the most common metric prefixes. The metric system has a variety of units of measurement - you have probably heard of meters (which measure distance) and grams (which measure mass), etc. These base units are sometimes either too small or too large to make practical measurements. In these cases, it's necessary to use units that differ from the base units by a power of 10 - in other words, measurements that are 10 times larger or smaller, 100 times larger or smaller, and so on. In these cases, we add prefixes to the name of the unit to signify how much bigger or smaller it is than the base unit.[1] The most common of these prefixes, from "1,000 times larger" to "1,000 times smaller," are:
Kilo - 1,000 times larger
Hecto - 100 times larger
Deca - 10 times larger
Deci - 10 times smaller
Centi - 100 times smaller
Milli - 1,000 times smaller
A handy trick for remembering the basic metric prefixes is the mnemonic "King Henry Died Until Drinking Chocolate Milk," (or, if you prefer, "King Henry Doesn't Usually Drink Chocolate Milk"). The first letter of each word corresponds to a basic metric prefix, in order of largest to smallest, except for the "U" in "Until", which corresponds to "unit," or the metric base units (meter, liter, etc.)
Step 2: List the prefixes on a line. If you're unfamiliar with metric units, it can be helpful to list the metric prefixes on a line in order of largest to smallest. Put "Kilo" at the far left end of the line and "Milli" at the far right end. In the middle of the scale, between "Deca" and "Deci," put the base unit of the dimension you're measuring. In other words, if you're measuring distance, write "meter," if you're measuring volume, write "liter," and so on. This line gives you a simple visual reference for how your units relate - whether the units you want are larger or smaller than the units you have, and how much larger or smaller they are.
Step 3: Determine whether the units you want are larger or smaller than the units you have. Look at your line of prefixes. Find the prefix that corresponds with the units you took your initial measurement in. Next, find your desired units. Are they to the right or to the left of your initial units? If they are to the right, you are converting from a larger unit into a smaller one. If they are to the left, you are going from a smaller unit to a larger one.
* For example, let's say that we want to know how long a 10-kilometer race is in centimeters. On our line of prefixes, we would see that "centi" is to the right of "kilo". Since our desired units are to the right of our initial units, we know we're converting from a large unit into a smaller unit.
Step 4: Determine the numerical relationship between the units you have and the units you want. Metric units of measurement differ by powers of 10 - 10, 100, 1,000, and so on. Thus, converting from one metric unit to another is always accomplished by multiplying or dividing your initial measurement by the appropriate power of ten. Look at the arrow you've drawn from the units you have - the units your measurement has been taken in - to the units you want to convert to. The number of spaces under your arrow gives the power of ten by which your two units are related.[3]
* For instance, in our 10-kilometer race example, we see that our arrow from "kilo" to "centi" jumps over five spaces. This means that kilometers and centimeters differ by a conversion factor of five powers of ten, also written as ten to the fifth power, 105, or 10 × 10 × 10 × 10 × 10 = 100,000. In other words, centimeters are 100,000 times (or 105, etc.) times smaller than kilometers. Thus, you know that there are 100,000 centimeters in 1 kilometer.
 |
| Photo: splashlearn |
Step 5: For "large to small" conversions, multiply by the appropriate power of ten. Converting from a large unit to a smaller unit means you should multiply your original measurement by the amount that its units differ from the desired final units. Remember that this number should be a power of ten given by the number of spaces under the arrow you drew in the steps above.
Sometimes, especially in schoolwork, it's not enough to simply give the correct number. You'll also be asked to show how you converted your initial unit label to its final form. In simple conversions like we're dealing with here, just label the units of your initial measurement as you normally would, then label your conversion factor with the fraction (desired units)/(units of your initial measurement). The units in the denominator will cancel with the units of your initial measurement, leaving your answer in terms of your desired units.
* In our 10-kilometer race example, we would simply multiply 10 (our initial measurement in kilometers) by 105 (or 100,000 - the number of centimeters in a kilometer). See below:
10 km × 105 cm/km =
10 km × 100,000 cm/km =
= 1,000,000 cm. There are 1,000,000 centimeters in our 10 kilometer race.
For "small to large" conversions, divide by the appropriate power of ten. Converting from a small unit to a larger unit is essentially the opposite process as the reverse - instead of multiplying, you'll need to divide. Take your initial measurement and divide it by the amount that its units differ from the desired final units - again, this should be a power of ten.
Step 6: Alternatively, you can multiply by the inverse power of ten to get the same results. For example, rather than dividing your measurement by 103, you would multiply it by 10-3. Both operations are valid and will give the same answer.
Let's do an example problem. Let's say we want to covert 360 centimeters to decameters. Since "centi" and "deca" are three spaces apart on the line of prefixes, we know that decameters are 103 times larger than centimeters. We would convert by dividing as follows:
360 cm / (103 cm/dam) =
360 cm / (1,000 cm/dam) =
= 0.36 dam. 360 centimeters make 0.36 decameters.
| Example 1: Convert 5 km to m. As 1 km = 1000 m Therefore, 5 km = 5 × 1000 = 5000 m Example 2: Convert 250 kg to milligrams. We know, 1 g = 1000 mg and 1 kg = 1000 g So, we first convert the kg to g as: 1 kg = 1000 g Therefore, 250 kg = 250 × 1000 g = 250,000 g Now, converting g to mg: 1 g = 1000 mg, therefore: 250,000 g = 250,000 × 1000 mg = 250,000,000 mg Example 3: Convert 250 ml to liters. 1 liter = 1000 ml Therefore, 450 ml = 450 ÷ 1000 = 0.45 liter |
Method 2: Converting Through Decimal Movement
Step 1: Determine the direction and size of the conversion. This quick method will allow you to simply and easily convert between metric units without having to perform any multiplication or division. To begin, all you need to know is whether you're converting from a small unit to a larger unit or vice versa, as well as the size of the conversion you're making - in other words, whether your desired units differ from your initial units by 101, 102, etc.[4]
* Both of these can be determined by counting spaces and/or drawing an arrow on a line of the metric prefixes. For example, if we want to convert from kilometers to decameters, we know that we're converting from a large unit to a small unit because we have to travel to the right along the line to get from "kilo" to "deca," and we know that decameters are 102 times smaller than kilometers because "kilo" and "deca" are separated by two spaces.
 |
| Photo: Wikihow |
Step 2: Move the decimal point in your measurement. Since two metric units always differ from each other by some multiple of ten, it's possible to make metric conversions simply by shifting your initial number's decimal point. When converting from a large unit to a smaller unit, shift the decimal point one digit to the right for each power of ten that your desired units differ from your initial units. When converting from a small unit to a larger unit, move the decimal place to the left. Remember that the power of ten by which your desired units differ from your initial units is given by the number of spaces apart the two units are on the line of prefixes.
- For example, let's say that we want to convert 1 kilometer into centimeters. Since we can tell from the line of prefixes that centimeters are 105 times smaller than kilometers, we move the decimal point in "1" five spaces to the right. See below:
- 1.0
- 10.0
- 100.0
- 1,000.0
- 10,000.0
- 100,000.0. There are 100,000.0. centimeters in 1 kilometer.
- You may also do the reverse - move a number's decimal to the left to convert to a larger unit.
Step 3: Add zeroes as necessary. When you move a number's decimal point, be sure to add zeroes for each space that you move the decimal point beyond the available digits. For instance, when converting 1 kilometer to centimeters, the decimal point is initially to the right of the number 1, as so: 1. Moving the decimal place to the right means you must insert a zero so that the number becomes 10.
- The same principal applies when moving a decimal point to the left - begin inserting zeroes when you move the decimal beyond the number's available digits. For instance, let's say we want to convert 1 millimeter into meters. Since meters are 103 times larger than millimeters, we would simply move the decimal three spaces to the left as below:
- 1.0
- 0.10
- 0.010. Notice that we add a zero to the left of the 1.
- 0.0010. We add another zero to get our final answer. There are 0.001 meters in 1 millimeter.
- Only add zeroes if you run out of digits when moving the decimal point. Inserting superfluous zeroes into the middle of a number can make your answer incorrect.
Excel CONVERT Function
 |
| Photo: exceljet.net |
Summary
The Excel CONVERT function converts a number in one measurement system to another. For example, you can use CONVERT to convert feet into meters, pounds into kilograms, Fahrenheit to Celsius, gallons into liters, and for many other unit conversions.
Purpose
Convert measurement units
Return value
A number in the new measurement system
Syntax
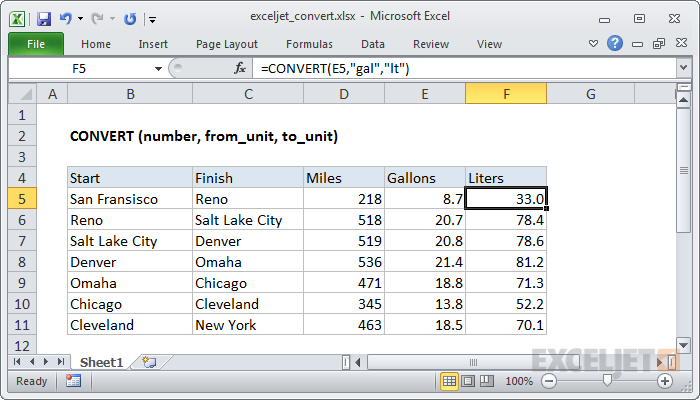
=CONVERT (number, from_unit, to_unit)
Arguments
number - The numeric value to convert.
from_unit - The starting units for number.
to_unit - The ending units for the result.
| Examples The formulas below use the CONVERT function to convert yards to meters, Celsius to Fahrenheit, gallons to liters, and square meters to square yards: =CONVERT(100,"yd","m") // returns 91.44 =CONVERT(22,"C","F") // returns 71.6 =CONVERT(1,"gal","l") // returns 3.79 =CONVERT(100,"m2","ft2") // returns 1076.39 |
Fun Facts
* A tonne is 1,000 kilograms.
* The metric system has its beginnings back 1670 by a mathematician called Gabriel Mouton.
* Since the 1960s the metric system is called the "International System of Units" or "SI" (from the French "Système International").
* The prefixes of the metric system can be remembered using the mnemonic “King Henry Died of Drinking Cold Milk”
* There are units greater than the kilo as well. These have prefix mega, giga and tera. A mega is 1000 times of kilo. A giga is 1000 times of mega and a tera is 1000 times of a giga.
In this video, you will learn more thoroughly about metric measurement system and ways to convert between them:
For more interesting news of KnowInsiders, check out right below!
 How to Convert PowerPoint to Word: Top 3 Simple Methods How to Convert PowerPoint to Word: Top 3 Simple Methods Sometimes it’s useful to convert your PowerPoint presentations into Word documents. Check out the detailed process of changing "PowerPoint to Word" with easy ways. |
 How to Convert PDF To Excel: Best Ways to Change How to Convert PDF To Excel: Best Ways to Change Your coworker sent you a PDF file instead of the Excel document you wanted, that doesn’t mean you’re actually stuck with it. In this guide, ... |
 How to Convert Word to PowerPoint: Top 3 Simple Methods How to Convert Word to PowerPoint: Top 3 Simple Methods PowerPoint is a great way to merge text and images for presentations. Are you struggling with the way to convert Word to Powerpoint? Check out ... |