How to Convert Degrees to Radians and Radians to Degrees: Best Ways to Change
 |
| Photo KnowInsiders |
Degrees and radians are two different units that are used for the measurement of the angles. The conversion of degrees to radians is considered while measuring the angles in Geometry. The measure of the angle is generally denoted by degrees, having the symbol °. An angle can be determined by two different kinds of units, that are, degrees and radians. You can convert one form of the representation of any mathematical angle to the other by using simple formulas. A degree also has its sub-parts that are minutes and seconds. This conversion plays a major part in the trigonometry applications. In this article, we will learn about how to convert degrees to radians, degrees to radians formula, and look at some solved examples based on how to convert degrees to radians formula. Let us first look at the degree to radian conversion.
What is a radian?
Okay, so radian is an angle with vertex at the center of a circle that intercepts an arc on the circle equal in length to the radius of the circle. Or as summarized by Teacher’s Choice, one radian is the angle of an arc created by wrapping the radius of a circle around its circumference.
 |
| Photo calcworkshop |
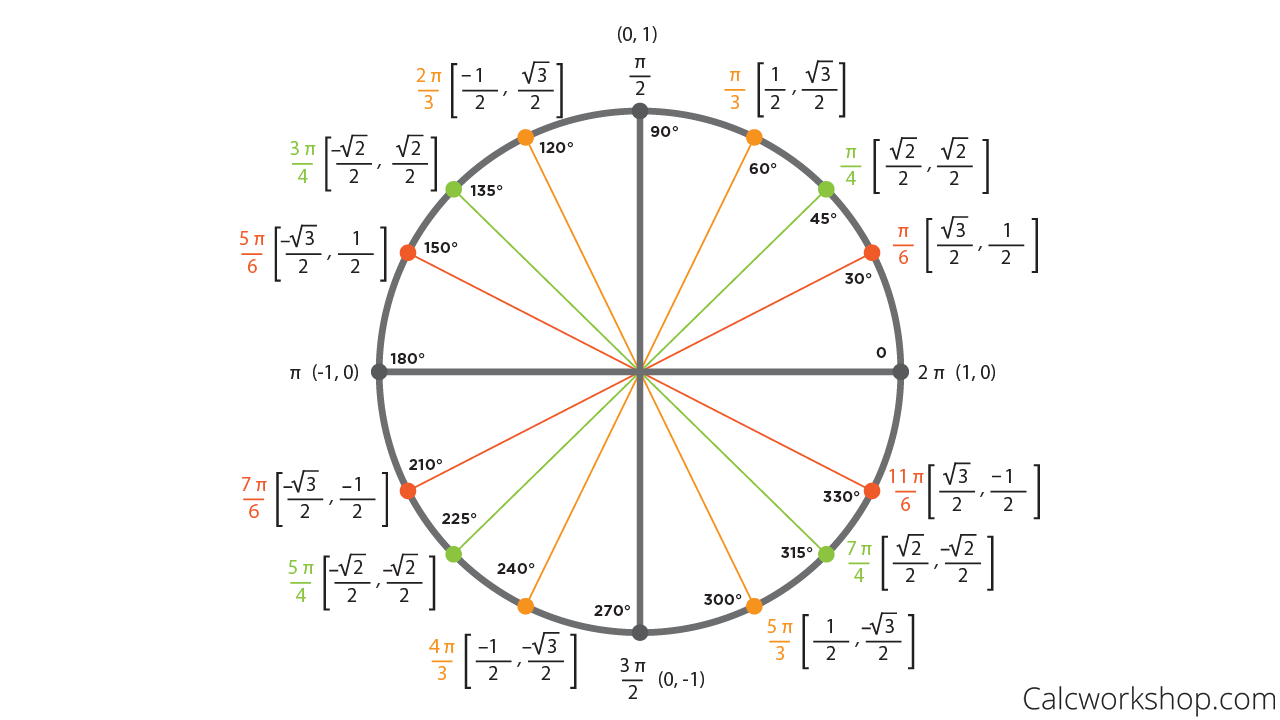
Picture a circle.
Now we know two things:
A circle has 360 degrees all the way around.
The circumference of any circle is just the distance around it. This means that the number of radii in the circumference is 2pi.
Which means that one trip around a circle is 360 degrees or 2pi radians!
 |
| Photo calcworkshop |
How to Convert Degrees to Radians - Updated
The value of 180° is equal to π radians. To convert any given angle from the measure of degrees to radians, the value has to be multiplied by π/180.
| Degrees to Radians Formula Degree x π/180 = Radian |
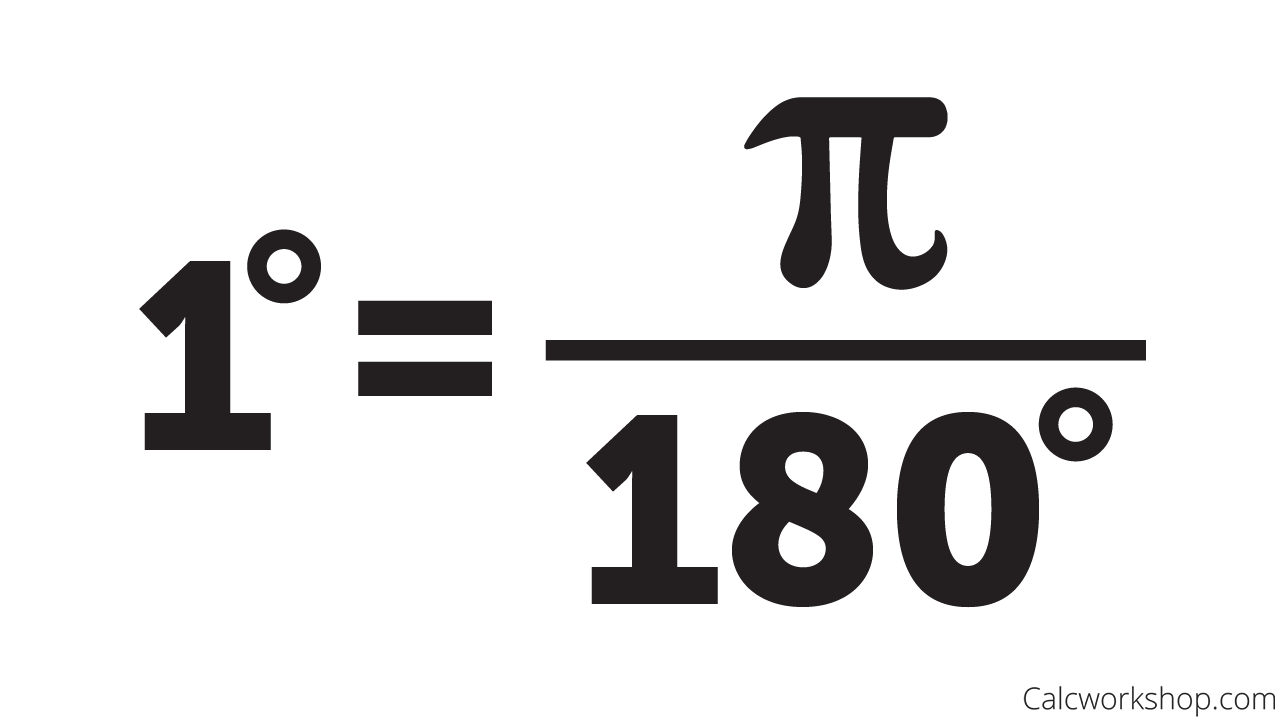 |
| Photo calcworkshop |
Below steps show the conversion of angle in degree measure to radians.
Step 1: Write the numerical value of measure of angle given in degrees
Step 2: Now, multiply the numeral value written in the step 1 by π/180
Step 3: Simplify the expression by cancelling the common factors of the numerical
Step 4: The result obtained after the simplification will be the angle measure in radians
| Example: Convert 90 degrees to radians. Solution: Given, 90 degrees is the angle Angle in radian = Angle in degree x (π/180) = 90 x (π/180) = π/2 Hence, 90 degrees is equal to π/2 in radian. |
How to Convert Radians to Degrees - Updated
As we have already discussed, how to convert degrees to radians for any specific angle. Now, let us see how we can convert radians to degrees for any specific angle. The formula to convert radians to degrees is given by:
| Radians × (180/π) = Degrees |
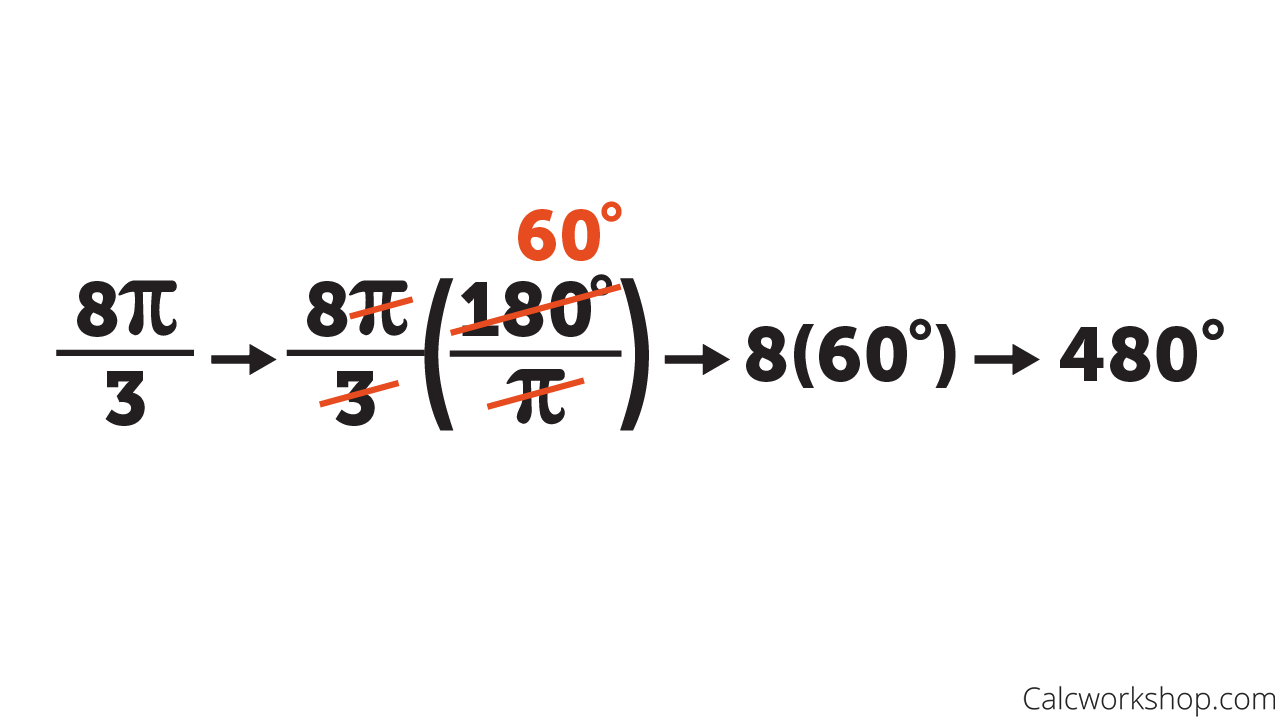 |
| Photo calcworkshop |
| Example: Convert π/6 into degrees. Solution: Using the formula, π/6 × (180/π) = 180/6 = 30 degrees |
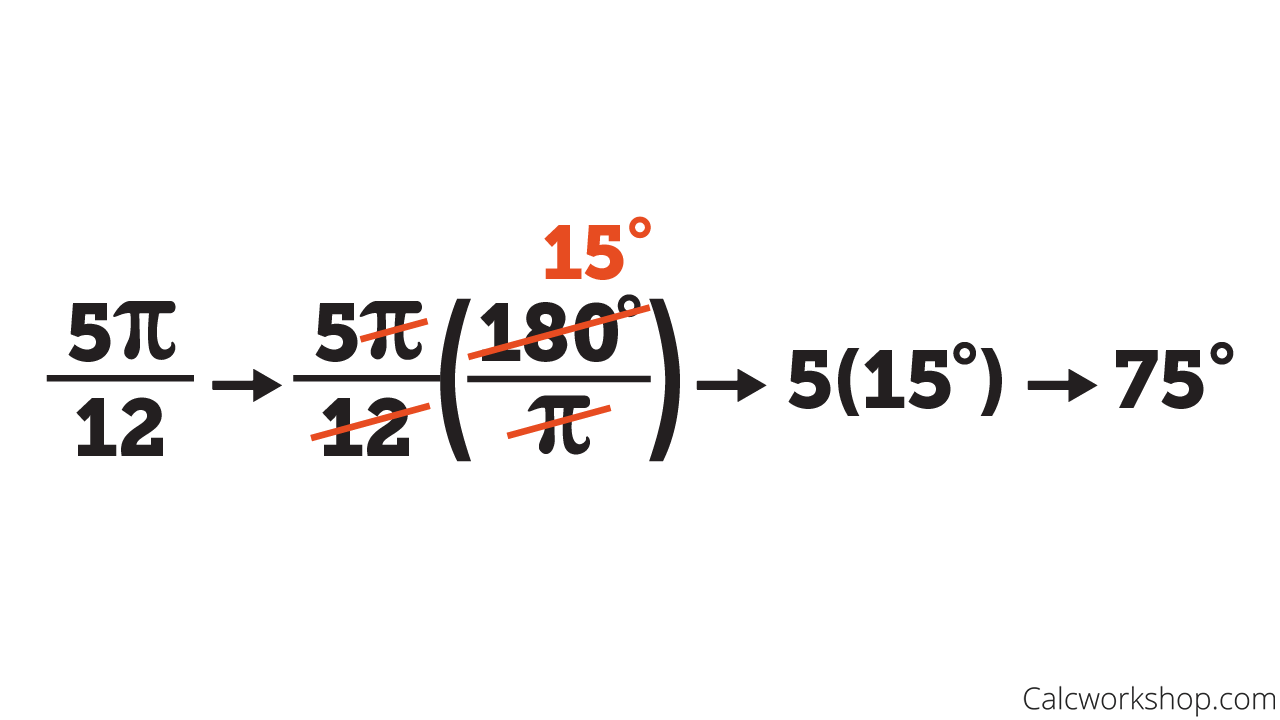 |
| Photo calcworkshop |
Radian to Degree Equation - Updated
As we know already, one complete revolution, counterclockwise, in an XY plane, will be equal to 2π (in radians) or 360° (in degrees). Therefore, both degree and radian can form an equation, such that:
2π = 360°
Or
π = 180°
| Example : Convert 15 degrees to radians. Solution: Using the formula, 15 x π/180 = π/12 |
| Example: Convert 330 degrees to radians. Solution: Using the formula, 330 x π/180 = 11π/6 |
Convert Negative Degrees to Radian- Updated
The method to convert a negative degree into radian is the same as we have done for positive degrees. Multiply the given value of the angle in degrees by π/180.
Suppose, -180 degrees has to be converted into radian, then,
Radian = (π/180) x (degrees)
Radian = (π/180) x (-180°)
Angle in radian = – π
Degrees to Radians Chart- Updated
Let us create the table to convert some of the angles in degree form to radian form.
Angle in Degrees Angle in Radians
0° 0
30° π/6 = 0.524 Rad
45° π/4 = 0.785 Rad
60° π/3 = 1.047 Rad
90° π/2 = 1.571 Rad
120° 2π/3 = 2.094 Rad
150° 5π/6 = 2.618 Rad
180° π = 3.14 Rad
210° 7π/6 = 3.665 Rad
270° 3π/2 = 4.713 Rad
360° 2π = 6.283 Rad
Question 1: Convert 200 degrees into radians.
Solution: By the formula, we know;
Angle in radians = Angle in degree × π/180
Thus,
200 degrees in radians = 200 × π/180 = 10π/9 = 3.491 Rad
Question 2: Convert 450 degrees into radians.
Solution: By the formula, we know;
Angle in radians = Angle in degree × π/180
Thus,
450 degrees in radians = 450 × π/180 = 7.854 Rad
| How to convert 30 degrees to radians? Multiply 30 degrees to π/180: 30 x (π/180) = π/6 Hence, 30 degrees is equal to π/6 in radians How pi radians is equal to 180 degrees? One complete revolution, counterclockwise, in an XY plane, will be equal to 2π (in radians) or 360° (in degrees). Hence, we can write: 2π = 360° Or π = 180° Therefore, pi is equal to 180 degrees What is the value of 1 degree?One degree is equal to 0.0174533 radians. What is the value of 1 radian? One radian is equal to 57.2958 degrees. Convert 3 radians to degrees. 3 radian × 180/π = 171.887Deg |
 How Many Ounces in A Cup of Water, Beer, Coffee, Rice and Flour? How Many Ounces in A Cup of Water, Beer, Coffee, Rice and Flour? Do you often cook? Have you ever wonder how to convert cups to ounces? Here you are. |
 How to teach your kids basic math skills How to teach your kids basic math skills Whether you're homeschooling or you just want to give your child a head start on math, it's easy to get your child to start thinking ... |